Example5:

Experiment has shown that the lifetime of a light bulb is exponentially distributed. Let X be the lifetime of a light bulb selected at random from the production line of a light bulb manufacturer. For simplicity, let us measure the lifetime in years, rather than hours, and suppose that the average light bulb produced by the manufacturer burns out in year of continuous use.

What proportion of the light bulbs will burn out within year?

What proportion will continue to burn for at least 1 year?

Solution:

The average value of X is , so we let and .

The proportion of light bulbs where X is less than or equal to is

.

The proportion of light bulbs that do not burn out for at least 1 year is

To evaluate this improper integral, we compute

as . Hence

Example6:

Suppose that we want to design a rectangular building having volume 147,840 cubic feet. Assuming that the daily loss of heat is given by

,

where x, y, and z are, respectively, the length, width, and height of the building, find the dimensions of the building for which the daily heat loss is minimal.

Solution:

We must minimize the function

, —(1)

Where x, y, z, satisfy the constraint equation

For simplicity, let us denote 147,840 by V. then xyz = V, so that z = V/xy. We substitute this expression for z into the objective function (1) to obtain a heat-loss function g(x, y) of two variables—namely

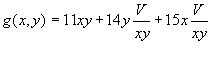
To minimize the function, we first compute the partial derivatives with respect to x and y; then we equate them to zero.

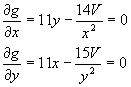
These two equations yield

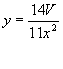—(2)

—(3)

If we substitute the value of y from (2) into (3), we see that

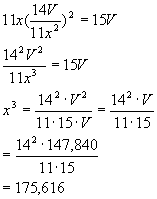
Therefore, we see that (using a calculator or a table of cube roots)

From equation (2) we find that

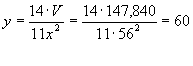
Finally,

Thus the building should be 56 feet long, 60 feet wide, and 44 feet high in order to minimize the heat loss.*

When considering a function of two variables, we find points (x, y) at which f(x, y) has a potential relative maximum or minimum by setting and equal to zero and solving for x and y. However, if we are given no additional information about f(x, y), it may be difficult to determine whether we have found a maximum or a minimum (or neither). In the case of functions of one variable, we studied concavity and deduced the second-derivative test. There is an analog of the second derivative test for functions of two variables, but it is much more complicated than the one-variable test. We state it without proof.

|Next|Back|Differentiation|Home|