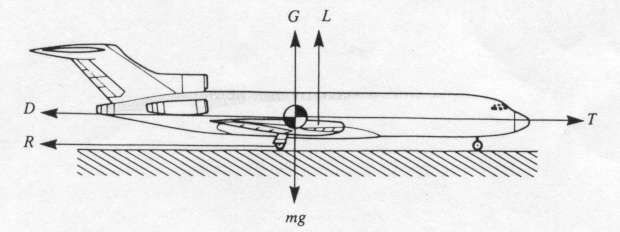
The Take-off run of an aircraft
Aeronautical engineers need to be able to predict the length of runway that an aircraft will require to take off safely. To do this, a mathematical model of the forces acting on the aircraft during the take-off run is constructed, and the relationships holding between the forces are identified. The figure below shows an aircraft and the forces acting on it. If the mass of the aircraft is m, gravity causes a downward force mg. There is a ground reaction force through the wheels, denoted by G, and an aerodynamic lift force L. The engines provide a thrust T, which is opposed by an aerodynamic drag D and a rolling resistance from contact with the ground R. Since the airforce is rolling along the runway, it is not accelerating vertically, so the vertical forces are in balance and the vertical equation of motion yields.
L + G = mg ------------------------------------(1)
On the other hand, the aircraft is accelerating along the runway, so the horizontal equation of the motion is
T - D - R = m
----------------------------(2)
where s is the distance the aircraft has travelled along the runway.
We know from experimental evidence that both aerodynamic lift and aerodynamic drag forces on a body vary roughly as the square of the velocity of the airflow relative to the body. We shall therefore choose to model the lift and drag forces as proportional to velocity squared. The rolling resistance is also known to be roughly proportional to the reaction force between ground and aircraft. Thus we make the modelling assumptions
L = a n
, D = b n
, and R = m G
Substituting for L, D and R in (1) and (2) and eliminating G results in the equation
m
- (m a - b )n
+ m mg = T
or replacing n by
m
- (m a - b )
= T - m mg-------------(3)
Thus our model of the aircraft travelling along the runway provides an equation relating the first and second time derivatives of the distance travelled by the aircraft, the thrust provided by the engines and various constants -- the model is expressed as a differential equation for the distance s travelled along the runway. The model is not yet really complete, since we have not specified how the thrust varies. The thrust could, of course, vary with time (the pilot could not open or close the throttles during the take-off run), and may also vary with the forward speed of the aircraft. On the other hand, we could just assume that thrust is constant. Also, the constants, m, m , a and b need to be determined. This information might be provided by the measurements on the aircraft or on scale models of it, by other calculations or engineers' estimates.