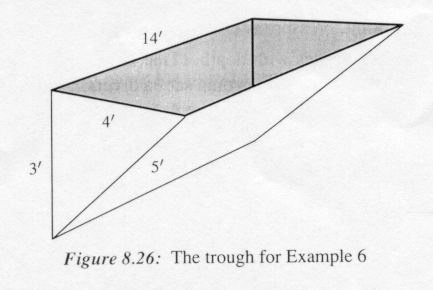
Example4:
A trough 14 feet long has one rectangular vertical side 14 feet by 3 feet, one rectangular inclined side 14 feet by 5 feet, and two triangular ends with sides 3 feet, 4 feet, and 5 feet (See Figure 8.26). If the trough is filled to the top with water, compute the force on each end and each side.
Solution:
We will do the long vertical side first. Divide the side into thin horizontal strips of
width 
. Since pressure depends only on the depth h and the
strips are thin and horizontal, we can assume the pressure is the same at every point in
the strip. The area of the strip is 
ft², and the force on the
strip at depth h ft is the pressure at that depth times the area of the strip:
Force on strip = Pressure 
Area 
lb/ft²
ft²
lb.
Summing the forces on these strips, we get an expression for the total force on the vertical side:
lb.
Letting 
, we get a definite integral. Since h varies
from 0 to 3 feet, we have
pounds.
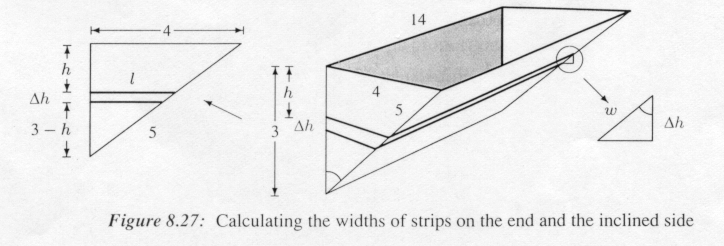
To compute the force on the inclined side, we use an inclined horizontal strip. Each
strip has length 14, but its width is not 
. By similar triangles
(see Figure 8.27) the width w of the strip satisfies
, so 
.
Therefore,
Area of strip = 
ft²,
So
Force on strip = 
lb.
The total force on the inclined side is obtained by adding the forces on the strips, giving
lb.
We let 
to arrive at a definite integral. Again, h varies
between 0 to 3 feet, so
pounds.
Notice that this is just 
the force on the vertical side.
Finally, to compute the force on each triangular end, we again divide the end into
horizontal strips. The width of the strip is as with the vertical
side, but this time the length of the strip varies from 4 feet at the top of the trough to
0 feet at the bottom. By similar triangles (see Figure 8.27) the length l of a
strip is related to the depth h by
, so 
.
Thus, the area of the strip is 
ft². As before, this means the
total force is
lb.
Since h varies between 0 to 3, as 
we have
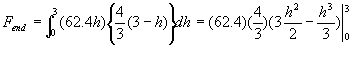
pounds.