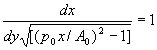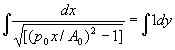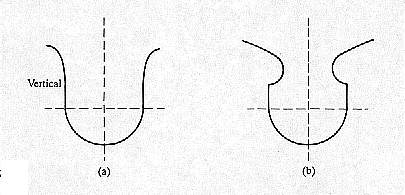Design of prismatic channel
The mean velocity V of flow in straight prismatic channels is proportional
to (A/p)r, where A is the cross-sectional area of the
flow, p is the wetted perimeter and r is approximately a constant (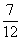 ). Given the channel section for minimum flows (that is A0
and p0),the objective is to design a channel such that V has the
same value for all larger discharges.
). Given the channel section for minimum flows (that is A0
and p0),the objective is to design a channel such that V has the
same value for all larger discharges.
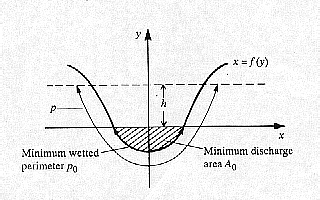
Assume a symmetric channel cross-section as shown below, where A0 and
p0 are the minimum flow value of A and p. Let the shape of
the channel be given by 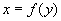 . (Note that in this application y, the
height of the surface above the datum line, is the independent variable.) Then we want to
find the function f(y)such that the mean flow velocity is independent of y. this
implies that
. (Note that in this application y, the
height of the surface above the datum line, is the independent variable.) Then we want to
find the function f(y)such that the mean flow velocity is independent of y. this
implies that 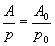 .
.
Solution:
The area A is given by the integral of f(y). Thus 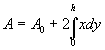 ,
where x=f(y) and h>0.
,
where x=f(y) and h>0.
The wetted perimeter p is given by 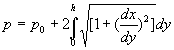 (h>0)
(h>0)
Since A/A0=p/p0, we deduce that 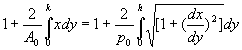
Rearranging the integrals under a common integral sign gives
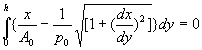 (h>0)since this is true for all h>0, it
implies that the integrand must be identically zero. Thus x=f(y) satisfies the
differential equation
(h>0)since this is true for all h>0, it
implies that the integrand must be identically zero. Thus x=f(y) satisfies the
differential equation 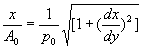 which implies
which implies 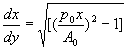 giving
giving
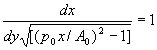
Integrating with respect to y then gives 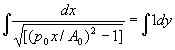
Using the substitution u = cosh (p0x/A0) on the left-hand side
gives
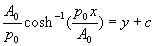
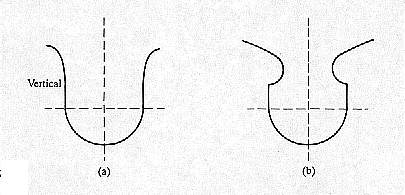
if the channel had width 2b where y=0, we can obtain the value of the
constant of integration c as 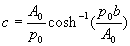 and deduce the formula for a
suitable channel shape as
and deduce the formula for a
suitable channel shape as 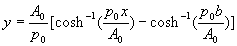 . This solution is not unique and we
note that the differential equation is satisfied by
. This solution is not unique and we
note that the differential equation is satisfied by 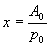 .
.
|Back|Differentiation|Home|
|History|Menu|More Sites|Quotations|Credits|
![]() ). Given the channel section for minimum flows (that is A0
and p0),the objective is to design a channel such that V has the
same value for all larger discharges.
). Given the channel section for minimum flows (that is A0
and p0),the objective is to design a channel such that V has the
same value for all larger discharges. 
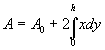 ,
where x=f(y) and h>0.
,
where x=f(y) and h>0.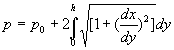 (h>0)
(h>0)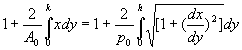
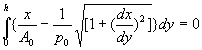 (h>0)since this is true for all h>0, it
implies that the integrand must be identically zero. Thus x=f(y) satisfies the
differential equation
(h>0)since this is true for all h>0, it
implies that the integrand must be identically zero. Thus x=f(y) satisfies the
differential equation 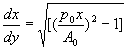 giving
giving