Integration3

Force and Pressure

We can use the definite integral to compute the force exerted by a liquid on a surface, for example, the force of water on a dam. The idea is to get the force from the pressure. The pressure in a liquid is the force per unit area exerted on a small piece of area in the liquid. Two things you need to know about pressure are:

At any point, pressure is exerted equally in all directions—up, down, sideways.

Pressure increases with depth. (That is one of the reasons why deep sea divers have to take much greater precautions than scuba divers.)

At a depth of h feet, the pressure exerted by the liquid measured in pounds per square foot, is given by computing the total weight of a column of liquid h feet high with a base of 1 square foot. The volume of such a column of liquid is just h cubic feet.

If the liquid has density (mass per unit volume), then its weight per unit volume is (where is the acceleration due to gravity). Thus the weight of the column of liquid is , so

Pressure = Density Depth

Sometimes you may be given the density of the liquid as a weight per unit volume, rather than a mass per unit volume. In that case, you do not need to multiply by because it has already been

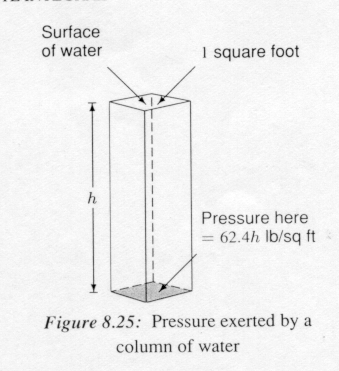
done. Since pounds are units of weight, and not mass, knowing that water weighs 62.4h lb/ft². (See figure 8.25.)

Next you need to know the relation between force and pressure. Provided the pressure is constant over a given area, we have the following relation:

Force = Pressure Area

When the pressure isn’t constant over a surface, we divide the surface into small pieces in such a way that the pressure is nearly constant on each one. Then we can use this formula on each piece and obtain a definite integral to get the force over an entire surface. Since the pressure varies with depth, we should divide the surface into horizontal strips, each of which is at an approximately constant depth.