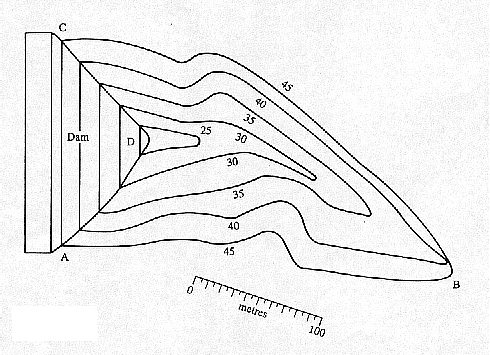
Consider the reservoir whose plan is shown below. Note from the contour lines that the
reservoir has a sloping wet face. By measuring the distance between the contour lines, we
can see that the slope on the face is constant. If A(h) denotes the surface area of
the water when it is at depth h, the capacity C of the reservoir is given by 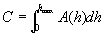
The area function A(h) can itself be expressed as an integral 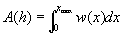 where w is the width of the surface at a distance x from
the dam. To estimate the capacity
where w is the width of the surface at a distance x from
the dam. To estimate the capacity 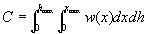
We estimate the area at each of the contour levels given in the plan by measuring the
widths at 10m intervals and applying the trapezium rule. Thus for the 45m contour we
obtain an estimate for the area ABC of the reservoir of 37760m2. The
corresponding estimates for the areas for 40, 35, 30 and 25 contours are 25060, 12470,
4520 and 660m2 respectively and the bottom of the reservoir at D is 22m above
the datum. Applying the trapezium rule again, taking care with the end point, we obtain an
estimate for the capacity of the reservoir: 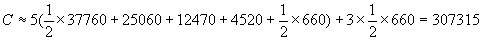
This expression is in cubic meters. In litres the capacity is approximately 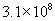 .
.
The process of numerical integration occurs in many engineering applications. We have
shown one approach: that of numerical integration in one variable or direction at a time.
Three other methods are commonly used:
a rectangular grid (suitable when boundaries are straight lines or planes),
a triangular grid (suitable for general boundaries),
the Monte Carlo method (suitable for complicated boundaries and a large number of
variables).
A full description of these methods is given by A. H. Stroud, Approximate Calculation
of Multiple Integrals (Prentice-Hall, Englewood Cliffs, NJ, 1996)
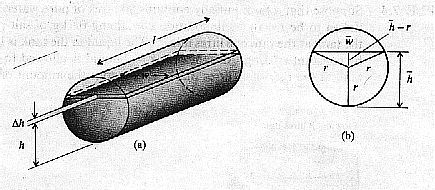
A cylindrical tank has circular cross-section of radius r (in m) and length l
(in m). It lies with its axis horizontal. The depth h (in m) of oil in the tank is
measured centrally, so that 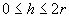 . When the tap at the bottom of the
tank is opened oil flows out at the rate
. When the tap at the bottom of the
tank is opened oil flows out at the rate 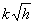 (in m3s-1),
where k is a constant. Find the corresponding rate at which the depth of the oil in
the tank is changing.
(in m3s-1),
where k is a constant. Find the corresponding rate at which the depth of the oil in
the tank is changing.
Solution:
Consider the outflow from the tank when the depth of oil drops from 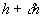 to h in a time interval
to h in a time interval 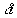 , as shown in
the diagram. The outflow in time
, as shown in
the diagram. The outflow in time 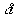 is (average velocity)
is (average velocity)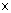 time; that is,
time; that is, 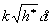 , where
, where 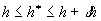
This must equal the loss in volume of oil in the tank, which is (average surface
area)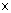 (change in depth); that is,
(change in depth); that is, 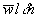 from
diagram (b), using Pythagoras’ theorem, the average width
from
diagram (b), using Pythagoras’ theorem, the average width 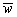 can be expressed in terms of the average height
can be expressed in terms of the average height 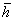 by
by
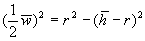 giving
giving 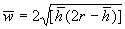
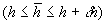
Then, equating the loss in volume with the outflow, we have
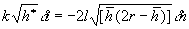 the negative sign indicating a loss or decrease in volume.
the negative sign indicating a loss or decrease in volume.
Simplifying, we have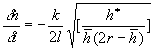 and letting
and letting 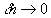 and so
that both
and so
that both 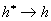 and
and 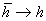 , we obtain the rate of
change of h with respect to t :
, we obtain the rate of
change of h with respect to t :
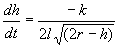
Note that in this example the rate of change of the dependent variable, namely the
depth of oil, is expressed in term of itself. This often happens in mathematical models of
practical problems.
|Next|Back|Integration|Home|
|History|Menu|More Sites|Quotations|Credits|
![]()


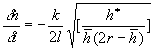 and letting
and letting