Suppose that a tank initially contains 80 liters of pure water. At a given instant
(taken to be t = 0) a salt solution containing 0.5 kg of salt per liters flows into
the tank at the rate of 8 liters min-1. The liquid in the tank is kept
homogeneous by constant stirring. Also, at time t = 0 liquid is allowed to flow out
from the tank at the rate of 12 liters min-1. Show that the amount of salt x(t)
(in kg) in the tank at time t (min) 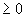 is determined by
is determined by
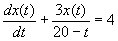
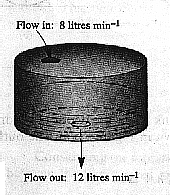
Figure (7.6)
Solution:
The situation is illustrated in Figure 7.6. Since x(t) denotes the amount of
salt in the tank at time 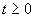 , the rate of increase of the amount of
salt in the tank is dx/dt, and is given by
, the rate of increase of the amount of
salt in the tank is dx/dt, and is given by
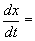 rate of inflow of salt — rate of outflow of
salt (7.4)
rate of inflow of salt — rate of outflow of
salt (7.4)
The rate of inflow of salt is 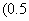 kg litre
kg litre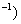
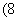 litres min
litres min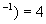 kg min
kg min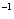
The rate of outflow of salt is c(rate of outflow of liquid) = c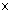 12 litres min
12 litres min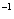
=12c (in kg min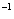 )
)
where c(t) is the concentration of salt in the tank (in kg litre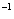 ). The concentration at time t is given by
). The concentration at time t is given by
c(t) = (amount of salt in the tank at time t )/(volume of
liquid in the tank at time t)
After time t (in min) 8t litres have entered the tank and 12t
litres have left. Also, at t = 0, there were 80 litres in the tank. Therefore the
volume V of liquid in the tank at time t is given by
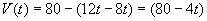
(Note that 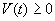 only if
only if 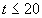 min; after this
time the liquid will flow out as quickly as it flows in and none will accumulate in the
tank.) Thus, the concentration c(t) is given by
min; after this
time the liquid will flow out as quickly as it flows in and none will accumulate in the
tank.) Thus, the concentration c(t) is given by
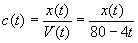
so that
rate of outflow of salt 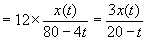
Substituting back into (7.4) gives the rate of increase as
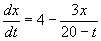
or
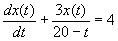
|Back|Integration|Home|
|History|Menu|More Sites|Quotations|Credits|
![]() is determined by
is determined by