Calculating the Work Done
In the following examples, we calculate the work done where both the force and distance moved may vary. To find the work done on a complicated object, we slice the object up in such a way that we can find the work done on each piece. We will calculate the work done for each piece using W = Fd, and we will sum these pieces to approximate the total work as a Riemann sum. Letting the size of each piece tend to zero, we will obtain a definite integral that represents the total work.
Example1:
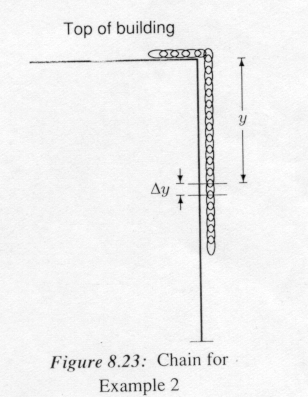
A 28-meter uniform chain with a mass of 20 kilograms is dangling from the roof of a building. How much work is needed to pull the chain up to the top of the building?

Solution:
Since a 20-kilogram chain weighs (20 kg)(9.8 m/sec²) = 196 newtons, it might seem that the answer should be (196 nt)(28 m) = 5488 joules. But remember that not all of the chain has to move 28 meters—links near the top move less.
Let’s divide the chain into small sections of length ![]() ,
each weighing 7
,
each weighing 7 ![]() newtons. (A length of 28 meters weighs 196
newtons, so 1 meter weighs 7 newtons.) See Figure 8.23. If
newtons. (A length of 28 meters weighs 196
newtons, so 1 meter weighs 7 newtons.) See Figure 8.23. If ![]() is
small, all of this piece is hauled up approximately the same distance, namely
is
small, all of this piece is hauled up approximately the same distance, namely ![]() , against the force due to gravity of 7
, against the force due to gravity of 7 ![]() newtons. Thus, the work done on the small piece is approximately
newtons. Thus, the work done on the small piece is approximately
(7![]() newtons)(
newtons)(![]() meters) = 7
meters) = 7
![]() joules.
joules.
The work done on the entire chain is given by the total of the work done on each piece:
![]()
![]() joules.
joules.
As ![]() tends to zero, we obtain a definite integral. Since
tends to zero, we obtain a definite integral. Since ![]() varies from 0 to 28 meters, the total work is
varies from 0 to 28 meters, the total work is
![]() joules.
joules.
Example2:
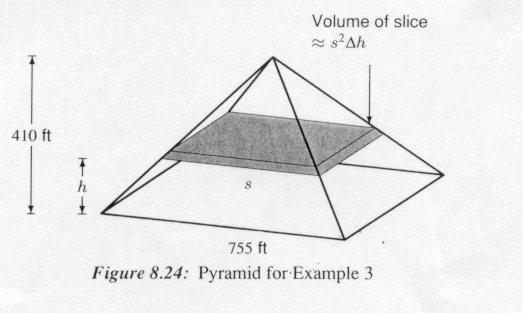
It is reported that the Great Pyramid of Egypt was built in 20 years. If the stone making up the pyramid has density 200 pounds per cubic foot, find the total amount of work done in building the pyramid. Estimate how many workers were needed to build the pyramid.
Solution:
We assume that the stones were originally located at the approximate height of the construction site. Imagine the pyramid was built in layers. Recall that the pyramid is 410 feet high and has a square base 755 feet by 755 feet.
We found by similar triangles that the layer at height ![]() has a
side length
has a
side length ![]() ft. The layer at height
ft. The layer at height ![]() has
a volume of
has
a volume of ![]() ft³ and hence a weight of
ft³ and hence a weight of ![]() lb.
Constructing this layer involved lifting a weight of
lb.
Constructing this layer involved lifting a weight of ![]() through a
height
through a
height ![]() , so the work required was (
, so the work required was (![]() lb)(
lb)(![]() ft) =
ft) = ![]() ft-lb. (See Figure 8.24.) The total
work, W, of constructing all the layers is then
ft-lb. (See Figure 8.24.) The total
work, W, of constructing all the layers is then
![]() ft-lb.
ft-lb.
As the thickness of each layer, ![]() , tends to zero, we obtain a
definite integral. Since
, tends to zero, we obtain a
definite integral. Since ![]() varies from 0 to 410, we have
varies from 0 to 410, we have
![]()
![]()
![]() foot-pounds.
foot-pounds.
We have calculated the total work done in building the pyramid; now we want to estimate
the total number of workers needed. Let’s assume every laborer worked 10 hours a day,
300 days a year, for 20 years. Assume that a typical worker lifted ten 50 pound blocks a
distance of 4 feet every hour, thus performing 2000 foot-pounds of work per hour (this is
a very rough estimate). Then each laborer performed ![]() foot-pounds
of work over a twenty-year period. Thus, the number of workers needed was about
foot-pounds
of work over a twenty-year period. Thus, the number of workers needed was about ![]() , or about 13,000.
, or about 13,000.