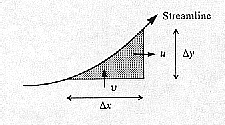
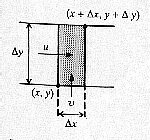
Consider the case of steady-state incompressible fluid flow in two dimensions. Using rectangular Cartesian coordinates (x,y) to describe a point in the fluid, let u and v be the velocities of the fluid in the x and y directions respectively. Then by considering the flow in and flow out of a small rectangle, as shown below, per unit time, we obtain a differential relationship between u(x,y) and v(x,y) that models the fact that no fluid is lost or gained in the rectangle; that is, the fluid is conserved.

Solution:

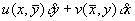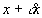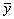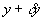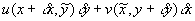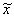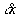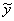The velocity of the fluid q is a vector point function. The values of its component u and v depend on the spatial coordinates x and y. the flow into the small rectangle in a unit time is where lies between x and , and lies between y and . Similarly, the flow out of the rectangle is where lies between x and x+and lies between y and 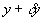. Because no fluid is created or destroyed within the rectangle, we may equate these two expressions, giving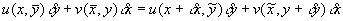

Rearranging, we have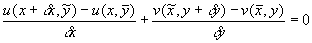

Letting and gives the continuity equation .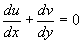

The fluid actually flows along paths called streamlines so that there is no flow across a streamline. Thus from the figure we can deduce that 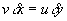and hence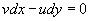

The condition for this expression to be exact differential is 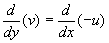or

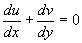
This satisfied for incompressible flow since it is just continuity equation, so that we deduce that there is a function 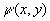, called the stream function, such that 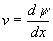and 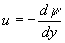. It follows that if we are given u and v, as functions of x and y, that satisfy the continuity equation then we can find the equations of the streamlines given by 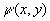=constant

Find the stream function y (x,y) for the incompressible flow that is such that the velocity q at the point (x,y) is (-y/(x²+y²), x/(x²+y²)).

Solution:

From the definition of the stream function, we have 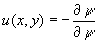and 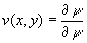provided that 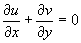. Here we have

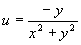and 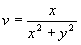so that 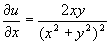and 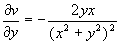confirming that 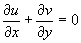integrating 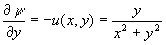with respect to y, keeping x constant, gives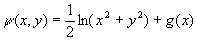

Differentiating partially with respect to x gives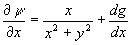

Since it is known that 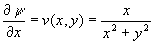we have 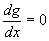which on integration gives g(x) =C where C is a constant. Substituting back into the expression obtained for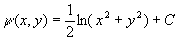

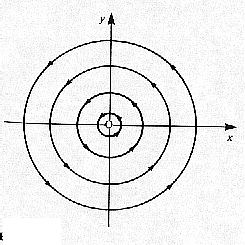
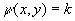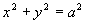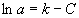A streamline of the flow is given by the equation , where k is a constant. After a little manipulation this gives and and the corresponding streamlines are shown in the given diagram. This is an example of a vortex.