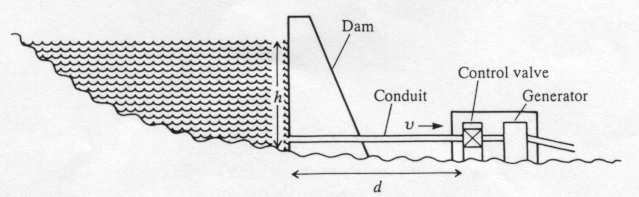
(iii) Hydro-electric power generation
Our third example is drawn from the sphere of hydraulic engineering. The figure below shows a cross-section through a hydropower generation plant. Water, retained behind a dam, is drawn off through a conduit and drives a generator. In order to control the power generated, there is also a control valve in series with the generator. The conduit from the dam to the generator is typically quite long and of considerable cross-section, so that it contains many tonnes of water. Hence, when the control valve is opened or closed, the power generated does not increase or decrease instantaneously. Because of the large mass of water in the conduit that must be accelerated or decelerated, the system may take several minutes or even tens of minutes to attain its new equilibrium flow rate and power generation level. We wish to predict the behaviour of the system when the control valve setting is changed.
The pressure at the entry to the conduit will be atmospheric plus r gh, where r is the density of the water in the dam and h is the depth of the entry below the water surface. It is known that for flow in pipes, to a good approximation, the volume flow rate is proportional to the pressure differential between the ends of the pipe. We express this as
Q = a D p
where Q is the volume flow rate through the conduit, a is a constant and D p
is the pressure difference between two ends of the conduit. It is also known that the pressure loss across the generator is also proportional to the discharge ( volume flow through the generator ), so we can write
D p
= b Q
where D p
D p
= g Q
where D p
- D p
. If this exceeds D p
, the pressure differential needed to maintain the flow through the conduit at its current level, then the mass of water will accelerate and the volume flow rate through the system will increase; if it is less than D p
then the mass of water will decelerate and the volume flow will decrease. The net force on the mass of water in the conduit is the excess pressure differential multiplied by the cross-sectional area of the conduit, A, say. The mass of water is r Ad, where d is the length of the conduit and Q, the volume flow rate, is Vd, where n is the velocity of the water in the conduit. Thus we can write
(r gh - D p
- D p
- D p
)A = r Ad
Assuming that the cross-sectional area of the conduit is constant and substituting for, D p
, we can re-write this as
(r gh -
- b Q - g Q)A = r d
that is,
+
Q = r gh
We find that this simple model of the hydro-power generation system results in an equation involving the volume flow rate through the system and its time derivative and, of course, various constants expressing physical characteristics of the system. One of these constants, g , is determined by the setting of the valve controlling the whole system.
