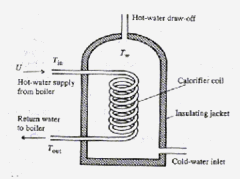
The second example involves modelling the heating of water in a hot-water storage tank. The figure below shows systematically an 'indirect' domestic hot-water tank. In this design of hot-water system the central heating boiler, or other primary source of heat, supplies hot water to a calorifier (which takes the form of a coiled pipe) inside the hot-water storage tank. The main mass of water in the tank is then heated by the hot water passing through the calorifier coil. We wish to calculate how quickly the hot water in the tank will heat up.
We shall assume that, to a good approximation, during heating convection ensures that the main mass of water in the tank is well mixed and at a uniform temperature T
. The heating water flows into the calorifier at a speed U at a temperature T
. The outflow from the calorifier is at temperature T
. The cross-sectional area of the calorifier tube is A. The mass flow rate of heating water through the calorifier is therefore r AU, where r is the density of water, and the
rate of heat loss from the heating water is r AU(T
r Vc
The tank is well insulated, so, to a first approximation, we shall assume that the heat loss from the external shell of the tank is negligible. The rate of heat gain of the main mass of water is therefore equal to the rate of heat loss from the heating water; that is,
AU (T
---------------------------(4)
We should also expect that the difference in temperature of the heating water flowing in and that flowing out of the calorifier will be greater the cooler the mass of water in the tank. If we assume direct proportionality of these two quantities, we may express this modelling assumption as
T
where a is a constant of proportionality. Eliminating T
V
Thus we have a differential equation relating the temperature of the water in the tank and its derivative with respect to time to the temperature of the heating water supplied by the boiler. The equation also involves various constants determined by the characteristics of the system.
